【ラビットチャレンジ】機械学習①:線形回帰モデル
1. はじめに
本記事は、ラビットチャレンジの機械学習①:線形回帰モデルに関する記事です。
ラビットチャレンジは、現場で潰しが効くディープラーニング講座の教材を活用した講座です。
詳細は以下のリンクをご確認ください。
2. 機械学習
機械学習について、説明したものは次の通り。
コンピュータプログラムは、タスクTを性能評価Pで測定し、その性能が経験Eにより
改善される場合、タスクTおよび性能指標Pに関して経験Eから学習すると言われている。
(トム・ミッチェル 1997)
つまり、ある評価指標において、あるタスクの性能が経験(過去データ)を使って、 性能が改善されるようならば、それを機械学習と定義している。
3.線形回帰モデル
ここでは、数ある機械学習モデルの中でも代表的な線形回帰モデルをとりあげる。
3.1 回帰問題
ある入力から出力を予測する問題。
直線なら線形回帰、曲線なら非線形回帰になる。
回帰で扱うデータは、次の2種類。
- x:説明変数(m次元ベクトル)
\(x = (x_1,x_2,\dots,x_n)^T\)
- y:目的変数(スカラー値)
\(y \in \mathbb{R}^1\)
説明変数(x)を使って、目的変数(y)を予測できるようにしていく。
回帰問題を当てはめるケースとして、住宅価格予測や来場者予測などがある。
住宅の例で言えば、部屋数、敷地面積や築年数などが説明変数、価格が目的変数となる。
3.2 線形回帰モデルの式
線形回帰のモデルでは、次のように定義する。
- w:パラメータ
\(w = (w_1,w_2,\dots,w_m)^T \in \mathbb{R}^m\)
- \(\hat{y}\):予測値
- \(w_0\):切片
\(\hat{y} = w^Tx + w_0 = \sum_j^mw_jx_j + w_0\)
xは既に手元にありますから、\(w\)と\(w_0\)求めれば、\(\hat{y}\)を出力することができる。
線形回帰モデルでは、上記の\(w\)と\(w_0\)を求める作業とイメージする。
3.3 誤差
実際に出力されている値は、誤差が加わって観測されていると仮定し、次の式を定義する。
- ε:誤差
\(y = w_0 + w_1x_1 + \dots + w_nx_n + ε\)
\(w\)と\(w_0\)を求めるには、yとxは既に分かっていますから、
εを最小化するように\(w\)と\(w_0\)を求めれば良いとわかります。
3.4 行列表現
実際のyやxは複数ある。
全部で、n個のデータがあるとすると、
\(y_1 = w_0 + w_1x_{11} + \dots + w_nx_{1n} + ε_1\)
\(y_2 = w_0 + w_1x_{21} + \dots + w_nx_{2n} + ε_2\)
\(\vdots\)
\(y_n = w_0 + w_1x_{n1} + \dots + w_nx_{nn} + ε_n\)
上記のように、n個の連立方程式ができる。
これを、行列を用いて表現すると、
\(y = Xw + ε\)
\(X = (x_1,x_2,\dots,x_n)^T\)
\(y = (y_1,y_2,\dots,y_n)^T\)
\(x_i = (1,x_{i1},\dots,x_{im})^T\)
\(ε = (ε_1,\dots,ε_n)^T\)
\(w = (w_0,w_1,\dots,w_m)^T\)
と表現できる。
3.5 最小二乗法
上記で表現したモデルのwを求める。
求めるには誤差εが最小となるようなwを計算する。
平均二乗誤差
データとモデルの出力誤差の和。
以下の式で定義される。
\(MSE = \frac{1}{n_{train}}\sum_{i=1}^{n_{train}}(\hat{y_i}^{(train)} - y_i^{(train)})^2\)
最小二乗法
上記誤差の式を利用し、
微分して0となるwを求めると次のようになる。
\(W = (X^{(train)T}X^{(train)})^{-1}X^{(train)T}y^{(train)}\)
解析的に、行列を用いてwが求まることが分かる。
上記のwは、最尤法による解と一致する。
よって、モデル式は、
\(\hat{y} = X(X^{(train)T}X^{(train)})^{-1}X^{(train)T}y^{(train)}\)
となる。3.6 モデル式の評価
回帰モデル式の評価方法として、MSEを使うこともあるが、 それ以外にも以下のような物がある。
決定変数
モデルの当てはまりの良さを示す指標。
最も当てはまりの良い場合は、1となる。
\(R^2(y,\hat{y}) = 1 - \frac{\sum_{i=1}^n(y_i - \hat{y}_i)^2}{\sum_{i=1}^n(y_i - \bar{y}_i)^2}\)
平均絶対誤差
実際の値と予測の値の絶対値を平均した物。
小さいほど誤差が少なく、正確に予測できていることを示す。
\(MAE(y,\hat{y}) = \frac{1}{n}\sum_{i=1}^{n}|y_i - \hat{y_i}|\)
二乗平均平方誤差
MSEの平方根をとったもの。
2乗した影響を平方根で補正する。
\(RMSE(y,\hat{y}) = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y_i}^2)}\)
4. 線形回帰のハンズオン
理論部分は、上記で終了です。
ここからは実際のデータを用いて、pythonで分析していくカリキュラムになっています。
scikit-learnを使用し、ボストン住宅価格データセットに対して回帰分析していきます。
4.1 モジュールとデータのインポート
スクリプト
#from モジュール名 import クラス名(もしくは関数名や変数名)
from sklearn.datasets import load_boston
from pandas import DataFrame
import numpy as np
# ボストンデータを"boston"というインスタンスにインポート
boston = load_boston()
ボストンデータ、pandas、numpyを読みこみます。
読み込んだボストンデータは、以下のような形式になっています。
#ボストンデータ出力
print(boston)
出力
{'data': array([[6.3200e-03, 1.8000e+01, 2.3100e+00, ..., 1.5300e+01, 3.9690e+02,
4.9800e+00],
[2.7310e-02, 0.0000e+00, 7.0700e+00, ..., 1.7800e+01, 3.9690e+02,
9.1400e+00],
[2.7290e-02, 0.0000e+00, 7.0700e+00, ..., 1.7800e+01, 3.9283e+02,
4.0300e+00],
...,
[6.0760e-02, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 3.9690e+02,
5.6400e+00],
[1.0959e-01, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 3.9345e+02,
6.4800e+00],
[4.7410e-02, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 3.9690e+02,
7.8800e+00]]),
'target': ...(省略)
}
「’ ‘:xxx」のうち’ ‘で囲まれているものは項目名、xxxは項目に対する値になっています。
項目のデータを取り出すときは、次のようにします。
スクリプト
#DESCR変数の中身を確認
print(boston['DESCR'])
出力
.. _boston_dataset:
Boston house prices dataset
---------------------------
**Data Set Characteristics:**
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
(省略)
DESCRは、ボストンデータの説明になっています。
上記を参考に、説明変数(特徴量)、目的変数を見ます。
スクリプト
#feature_names変数の中身を確認
#カラム名
print(boston['feature_names'])
出力
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
スクリプト
#data変数(説明変数)の中身を確認
print(boston['data'])
出力
[[6.3200e-03 1.8000e+01 2.3100e+00 ... 1.5300e+01 3.9690e+02 4.9800e+00]
[2.7310e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9690e+02 9.1400e+00]
[2.7290e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9283e+02 4.0300e+00]
...
[6.0760e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 5.6400e+00]
[1.0959e-01 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9345e+02 6.4800e+00]
[4.7410e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 7.8800e+00]]
スクリプト
#target変数(目的変数)の中身を確認
print(boston['target'])
出力
[24. 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 15. 18.9 21.7 20.4
18.2 19.9 23.1 17.5 20.2 18.2 13.6 19.6 15.2 14.5 15.6 13.9 16.6 14.8
18.4 21. 12.7 14.5 13.2 13.1 13.5 18.9 20. 21. 24.7 30.8 34.9 26.6
・・・
14.1 13. 13.4 15.2 16.1 17.8 14.9 14.1 12.7 13.5 14.9 20. 16.4 17.7
19.5 20.2 21.4 19.9 19. 19.1 19.1 20.1 19.9 19.6 23.2 29.8 13.8 13.3
16.7 12. 14.6 21.4 23. 23.7 25. 21.8 20.6 21.2 19.1 20.6 15.2 7.
8.1 13.6 20.1 21.8 24.5 23.1 19.7 18.3 21.2 17.5 16.8 22.4 20.6 23.9
22. 11.9]
dataの中身は、左からCRIM、ZN、INDUS、・・・と続いており、それらの値であることがわかります。
targetはそれぞれの行に対する価格であることがわかります。
4.2 データフレームの作成
上記の形式では少々見にくいため、見やすいデータフレーム形式で表すことにします。
データフレームを利用するには以下のようにします。
# 説明変数らをDataFrameへ変換
df = DataFrame(data=boston.data, columns = boston.feature_names)
# 目的変数をDataFrameへ追加
df['PRICE'] = np.array(boston.target)
# 最初の5行を表示
df.head(5)
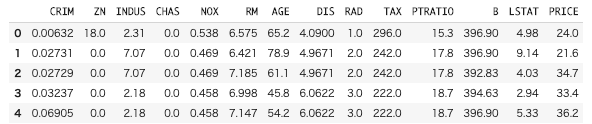
df.head()で上から指定した行数分を出力します。
データフレーム形式で見るとわかりやすく、
列ごとの値や各行が1個分のデータであることなどがわかります。
基本的に分析をするときは、このデータフレームの形式で行っていくようです。
4.3 線形単回帰分析
さて、線形回帰モデルの作成に入っていきます。
まずは、説明変数1個で単回帰分析を行っていきます。
#カラムを指定してデータを表示
df[['RM']].head()
# 説明変数
data = df.loc[:, ['RM']].values
#dataリストの表示(1-5)
data[0:5]
array([[6.575],
[6.421],
[7.185],
[6.998],
[7.147]])
先ほどのデータフレームからRMのみを取り出しています。
これが説明変数となります。
# 目的変数
target = df.loc[:, 'PRICE'].values
target[0:5]
array([24. , 21.6, 34.7, 33.4, 36.2])
価格を取り出します。
これが、目的変数となります。
## sklearnモジュールからLinearRegressionをインポート
from sklearn.linear_model import LinearRegression
# オブジェクト生成
model = LinearRegression()
# fit関数でパラメータ推定
model.fit(data, target)
回帰モデル式の部分です。
なんと、わずか3行で、回帰モデル式が計算されます。
便利ですね。
実際に値を予測するときは、以下のようにします。
#予測
model.predict([[1]])
array([-25.5685118])
用いている変数はRM(平均部屋数)ですから、
RMが1の住宅価格は-25(単位:$1000)となっています。
通常、価格が負とはならないので、うまく予測できてないことが伺えます。
実際、次の価格の分布を見ても価格が負のものはないので、モデルの精度は悪いのでしょう。
#予測
df["PRICE"].describe()
count 506.000000
mean 22.532806
std 9.197104
min 5.000000
25% 17.025000
50% 21.200000
75% 25.000000
max 50.000000
df.describe()で上記のような分布表を出してくれます。
決定変数とMSEを見ます。
# 平均二乗誤差を評価するためのメソッドを呼び出し
from sklearn.metrics import mean_squared_error
y_pred = model.predict(data)
y_true = target
#平均二乗誤差を出力
print('MSE: %.3f' % (mean_squared_error(y_true, y_pred)))
#R^2を出力
print('R^2: %.3f' % (model.score(data, target)))
MSE: 43.601
R^2: 0.484
MSEは0に近づく、決定変数は1に近づくほどモデルの精度は良いと判断できるため、
上記の場合、モデル精度は悪いということになります。
今回の場合、価格を決める要因は部屋数だけでは足りないと思われるので、
変数を増やしていけば精度が向上できると思われます。
4.4 重回帰分析
説明変数を1個増やして、2個にします。 CRIM(犯罪率)を増やします。
# 説明変数
data2 = df.loc[:, ['CRIM', 'RM']].values
# 目的変数
target2 = df.loc[:, 'PRICE'].values
# オブジェクト生成
model2 = LinearRegression()
# fit関数でパラメータ推定
model2.fit(data2, target2)
y_pred = model2.predict(data2)
y_true = target2
#平均二乗誤差を出力
print('MSE: %.3f' % (mean_squared_error(y_true, y_pred)))
#R^2を出力
print('R^2: %.3f' % (model2.score(data2, target2)))
MSE: 38.668
R^2: 0.542
MSEが減少、R^2が増加していることから、モデルの精度向上ができました。
さらに変数を増やしていくことで、モデルの精度は向上していくことが考えられます。
5. おまけ
講座のハンズオンでは、以上で終わっていますが、
なんだか味気ないので、もう少しいろいろやっていきましょう。
5.1 全部の変数を使う
2変数だけでなく、与えられている変数13個を使って回帰分析を行うとどうでしょうか。
変数を増やすと、精度向上が見込めそうに思えます。
スクリプト
# 説明変数
data3 = df.drop("PRICE",axis=1)
# 目的変数
target3 = df['PRICE']
# オブジェクト生成
model3 = LinearRegression()
# fit関数でパラメータ推定
model3.fit(data3, target3)
y_pred = model3.predict(data3)
y_true = target3
#平均二乗誤差を出力
print('MSE: %.3f' % (mean_squared_error(y_true, y_pred)))
#R^2を出力
print('R^2: %.3f' % (model3.score(data3, target3)))
出力
MSE: 21.895
R^2: 0.741
MSEが大きく減少、R^2は1に近づいていることからモデルの精度が向上しました!
特徴量を増やすことは、モデルの精度をあげることに繋がることが再度確認できました。
5.2 スケーリングを行う
もう1度、テーブルを見てみましょう。

各列ごとに値のスケールがバラバラに感じます。
例えば、CRIMが0.00632なのに対して、TAXは296.0になっています。
桁数で言えば5桁も差があります。
直感的によくなさそうなので、揃えることにしましょう。
揃え方はいろいろあるのですが、ここでは標準化を行います。
- μ:平均
- σ:標準偏差
\(x' = \frac{x - μ}{σ}\)
スクリプト
from sklearn.preprocessing import StandardScaler
#学習データに対して標準化を定義
scaler = StandardScaler()
scaler.fit(data3)
#変換のデータ
data3_trans = scaler.transform(data3)
data4 = DataFrame(data=data3_trans, columns = data3.columns)
data4.head(5)
出力

スケールは揃っている感じがします。
評価はどうでしょうか。
スクリプト
# オブジェクト生成
model4 = LinearRegression()
# fit関数でパラメータ推定
model4.fit(data4, target3)
y_pred = model4.predict(data4)
y_true = target3
#平均二乗誤差を出力
print('MSE: %.3f' % (mean_squared_error(y_true, y_pred)))
#R^2を出力
print('R^2: %.3f' % (model4.score(data4, target3)))
出力
MSE: 21.895
R^2: 0.741
変わらなかったですね。。
ここで、パラメータ(回帰係数)をみてみましょう。
スクリプト
model3.coef_
model4.coef_
出力
model3のパラメータ:
array([-1.08011358e-01, 4.64204584e-02, 2.05586264e-02, 2.68673382e+00,
-1.77666112e+01, 3.80986521e+00, 6.92224640e-04, -1.47556685e+00,
3.06049479e-01, -1.23345939e-02, -9.52747232e-01, 9.31168327e-03,
-5.24758378e-01])
model4のパラメータ:
array([-0.92814606, 1.08156863, 0.1409 , 0.68173972, -2.05671827,
2.67423017, 0.01946607, -3.10404426, 2.66221764, -2.07678168,
-2.06060666, 0.84926842, -3.74362713])
パラメータは変わっています。
これは、今回、直接的な評価に影響はありませんでしたが、
後にでてくる正則化する際に影響がありそうと考えられそうです。
5.3 多重共線性
以下の様に入力すると、変数間の相関係数をヒートマップ形式で出力してくれます。
スクリプト
df.corr().style.background_gradient(axis=None)
出力
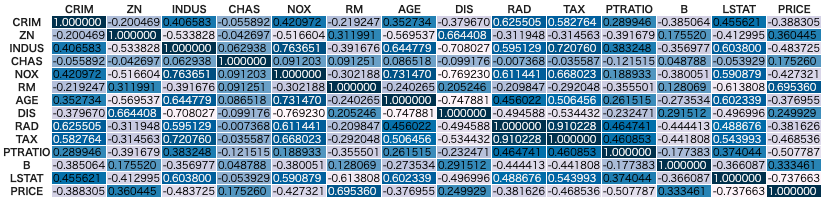
表を見ると、各PRICEとの相関係数の大きさが確認できます。
一方で、変数間の相関係数に着目すると、RADとTAXが0.91と高くなっています。
この様な変数間が強く相関しているケースを多重共線性(マルチコ)と呼ばれることがあります。
この問題として、パラメータの分散がおかしくなったり、有意差検定がおかしくなったりします。
上記の例で簡単に言えば、TAXとRADは価格に影響がある、効果がある、
みたいなことを強く言えなくなってしまいます。
基本的に、機械学習では各パラメータの解釈より、最終的な予測精度を重視する傾向にあるため、
それほど問題にならないケースが多いです。
また、後ほど出てくる正則化でこの問題に対処します。
一般的な対策として、
- 相関している変数のどちらかを削除する
- サンプル数を増やす
といったことが挙げられます。
5.4 評価指標
今回、評価指標としてMSEを使用しました。
この評価指標は、式で確認した通り、予測値と実測値の差分を2乗しています。
2乗することにより、元々の単位が変わってしまっているためあまり好ましくないです。
そのため、今回用いる指標は単位が同じであるRMSEもしくはMAEが良さそうです。
これらの特徴は、RMSEの場合は外れ値の影響を受けやすく、
MAEは影響を受けにくいといったことが挙げられます。(2乗しているかしていないか。)
使い分けとしては、例えば
- 大きな誤差を出すサンプルをできるだけ少なくしたい場合はRMSE
- 全サンプルの誤差を平等に評価して、サンプル全体の誤差をできるだけ
小さくしたいならMAE
となる様です。
今回の場合ですとRMSEが良さそうです。
以下に、RMSEによる評価を出力します。
スクリプト
#RMSE
print('RMSE model: %.3f' % (np.sqrt(mean_squared_error(y_true, y_pred))))
出力
RMSE model:6.603
RMSE model2:6.218
RMSE model3:4.679
RMSE model4:4.679
RMSEを出力する際は、MSEに平方根をとるようにして出力します。
上記の結果から、model3もしくはmodel4が良さそうですね。
また、今回は学習データ全てを学習させていますが、
本来なら学習データと検証データに分けて評価していきます。(ホールド・アウト法)
この方法は、次回の非線形回帰モデルの部分でまとめていきます。
6. 最後に
ラビットチャレンジでの講義である線形回帰モデルについてまとめました。
線形回帰モデルについては代表的な手法なので抑えておきたいですね。
初学者向けの講座なのか、あまり詳しい実装の解説はないようです。
scikit-learnを使わず実装する部分も試験範囲なので、見直しをしていきます。
また、いつものごとく色々数学的に突っ込みどころがありそうなまとめ方ですが、
ご了承ください。。
次回、機械学習②:非線形回帰モデルについてまとめていきたいと思います。
7. 参考リンク
scikit-learnで回帰モデルの結果を評価する
分析のお話 多重共線性ってなんだったんだっけ?
回帰分析の評価指標


