1. はじめに

本記事は、ラビットチャレンジの機械学習①：線形回帰モデルに関する記事です。
ラビットチャレンジは、現場で潰しが効くディープラーニング講座の教材を活用した講座です。
詳細は以下のリンクをご確認ください。

Deep Learning ラビット★チャレンジβ

現場で潰しが効くディープラーニング講座

2. 非線形回帰モデル

ここでは、線形でない場合の非線形回帰モデルをとりあげる。　　

2.1 基底展開法

非線形の場合、基底展開法を用いてモデリングを行う。

基底関数
ある関数を表現するの基底ベクトルのこと。
対象となる空間に属する全ての元（関数）は、この基底関数の線形結合で表される。

この基底関数と呼ばれる非線形関数とパラメータベクトルの線形結合を使用。
未知パラメータは最小二乗法や最尤法により推定する。

　　　　\(y_i = f(x_i) + ε_i\)

　　　　\(y_i = w_0 + \sum_{j=1}^mw_jφ_j(x_i) + ε_i\)

基底関数として、使われるものは次の通り。

• 多項式基底

　　　　\(φ_j(x) = x^j\)

• ガウス型基底関数

　　　　\(φ_j(x) = \exp(\frac{(x - μ_j)^2}{2h_j})\)

• スプライン関数/Bスプライン関数

2.2 モデル式

基底展開法も線形回帰と同じ枠組みで推定可能

• 説明変数

　　　　\(x_i = （x_{i1},x_{i2},\dots,x_{im}）\in \mathbb{R}^m\)

• 非線形関数ベクトル

　　　　\(φ(x_i) = （φ（x_{i1}）,φ（x_{i2}）,\dots,φ（x_{ik}））^T\in \mathbb{R}^k\)

• 非線形関数の計画行列

　　　　\(Φ^{(train)} = （Φ（x_1）,Φ（x_2）,\dots,Φ（x_n））^T\in \mathbb{R}^{n×k}\)

• 最尤法による予測値

　　　　\(\hat{y} = Φ（Φ^{(train)^T}Φ^{(train)}）^{-1}Φ^{(train)^T}y^{(train)}\)

2.3　未学習と過学習

未学習（underfitting）
学習データに対して、十分小さな誤差が得られないモデル

対策

• 表現力の高いモデルを採用
• 特徴量を増やす

など

過学習（overfitting）
小さな誤差は得られたが、テスト集合誤差との差が大きいモデル

対策

• 学習データの数を増やす
• 不要な基底関数（変数）を削除して表現力を抑止
• 正則化法を利用して表現力を抑止

など

2.4　正則化法

モデルの複雑さに伴って、その値が大きくなる正則化項（罰則項）を化した関数を最小化

　　　　\(S_γ = (y - Φw)^T(y - Φw) + γR(w)\)

• γR（w）:正則化項
  形状によっていくつもの種類があり、それぞれ推定量の性質が異なる。

• γ：正則化パラメータ
  モデルの曲線の滑らかさを調節

上記関数を最小化するすように学習を行っていく。

Ridge回帰
正則化項にL2ノルムを使用したものをRidge回帰と呼ぶ。
L2ノルムは、ベクトル差分の２乗和の平方根で、ユークリッド距離。

　　　　\(S_γ = (y - Φw)^T(y - Φw) + γ||w||_2\)

Lasso回帰
正則化項にL1ノルムを使用したものをLasso回帰と呼ぶ。
L1ノルムは、ベクトル成分の絶対値の和、マンハッタン距離。

　　　　\(S_γ = (y - Φw)^T(y - Φw) + γ||w||_1\)

最小化を考えたとき、パラメータwの影響が大きくなるため、
wの大きさをより引き下げる方向に進んでいく。

特徴
Ridge回帰の特徴は、なめらかな関数になる。
過学習を抑えることができる。

Lasso回帰の特徴は、一部のパラメータが0になる。
そのため、スパース推定とも呼ばれる。
不要なパラメータを削ることができる。

2.5 ホールドアウト法とクロスバリデーション法（交差検証）

ホールドアウト法
データを学習用とテスト用の2つに分割し、予測精度や謝りりつを推定するために使用

• 大体7:3で分けることが多い
• さらに、学習用、検証用、テスト用と分割することがある（６：３：１）
• 手元に大量にデータがない場合、良い性能評価を与えないという欠点がある

基底展開法に基づく非線形回帰モデルでは、基底関数の数、位置、チューニングを
ホールドアウト値を小さくするモデルで決定する。

クロスバリデーション法（交差検証）
イテレーターごとにデータを学習用と検証用に分割し、検証用データを評価し平均をとる。

例えば、5分割する場合、
　一回目：データセットに対し１を検証用、残り４を学習用とする。
　二回目：一回目で使った物以外の１を検証用、残り４を学習用とする。
　三回目：一回目、二回目で使った物以外の１を検証用、残り４を学習用とする。
という風に分割数分まで続いていく。

それぞれの検証用データに対し精度を評価し、精度の平均をとる。
これをCV値と呼ぶ。

ホールドアウト法で70%、クロスバリデーション法で65%の場合、
汎化性能は65%と判断した方が望ましい。

3. 非線形回帰のハンズオン

理論部分は、上記で終了です。
ここからはpythonで分析していくカリキュラムになっています。

3.1 必要モジュールのインポートとデータ準備

スクリプト

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

%matplotlib inline

#seaborn設定
sns.set()
#背景変更
sns.set_style("darkgrid", {'grid.linestyle': '--'})
#大きさ(スケール変更)
sns.set_context("paper")

いつも通り、必要モジュールをimportします。
今回からseabornを使っていく様です。
seabornはグラフを描画するライブラリになっています。

また、%matplotlin inlineは、ノートブック上で
グラフ描写を可能にするマジックコマンドです。

スクリプト

n=100

def true_func(x):
    z = 1-48*x+218*x**2-315*x**3+145*x**4
    return z

def linear_func(x):
    z = x
    return z

# 真の関数からノイズを伴うデータを生成

# 真の関数からデータ生成
data = np.random.rand(n).astype(np.float32)
data = np.sort(data)
target = true_func(data)

# 　ノイズを加える
noise = 0.5 * np.random.randn(n)
target = target  + noise

# ノイズ付きデータを描画

plt.scatter(data, target)

plt.title('NonLinear Regression')
plt.legend(loc=2)

出力結果

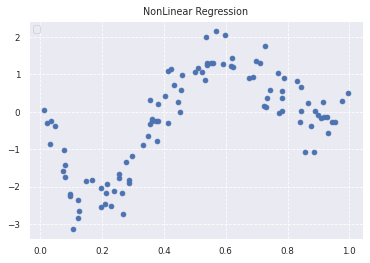
true_funcで、非線形の関数を定めます。
100個のランダムな初期値を作成し、true_funcを用いてデータを作成します。
ただ、このままだと真の分布に沿ったデータを作成していることになるので、
ノイズを加えて行きます。

上記のデータの分布を実際にプロットすると、非線形上のグラフができていることがわかります。

3.2 線形回帰による分析

スクリプト

from sklearn.linear_model import LinearRegression

clf = LinearRegression()
data = data.reshape(-1,1)
target = target.reshape(-1,1)
clf.fit(data, target)

p_lin = clf.predict(data)

plt.scatter(data, target, label='data')
plt.plot(data, p_lin, color='darkorange', marker='', linestyle='-', linewidth=1, markersize=6, label='linear regression')
plt.legend()
print("R^2：",clf.score(data, target))

出力結果

R^2：0.3286645739757943  

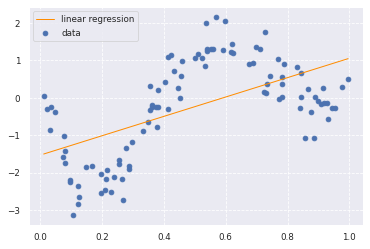
前回行った線形回帰で推定しています。
予想通り、線形回帰ではうまく予測できていないことが伺えます。
決定変数も0.32とかなり低いです。

3.3 非線形回帰による分析

スクリプト

from sklearn.kernel_ridge import KernelRidge

clf = KernelRidge(alpha=0.0002, kernel='rbf')
clf.fit(data, target)

p_kridge = clf.predict(data)

plt.scatter(data, target, color='blue', label='data')

plt.plot(data, p_kridge, color='orange', linestyle='-', linewidth=3, markersize=6, label='kernel ridge')
plt.legend()

出力

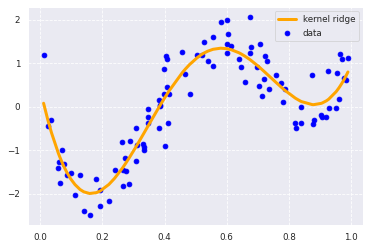
リッジ正則化とガウス型基底関数を用いて非線形回帰分析を行っています。
グラフを見ると、うまくデータにフィットしており良いモデリングといえそうです。
決定変数を見ていきましょう。

スクリプト

print("R^2：",clf.score(data,target))

出力

R^2： 0.8632333292346079

上記の通り、1に近づいており、線形回帰よりも精度がかなり向上しています。

ラッソ回帰の場合は以下の通りです。

スクリプト

#Lasso
from sklearn.metrics.pairwise import rbf_kernel
from sklearn.linear_model import Lasso

kx = rbf_kernel(X=data, Y=data, gamma=4)

lasso_clf = Lasso(alpha=0.0001, max_iter=1000)
lasso_clf.fit(kx, target)

p_lasso = lasso_clf.predict(kx)

plt.scatter(data, target)

plt.plot(data, p_lasso, color='green', linestyle='-', linewidth=3, markersize=3)

print("R^2:",lasso_clf.score(kx, target))

出力

R^2：0.8486233621864765

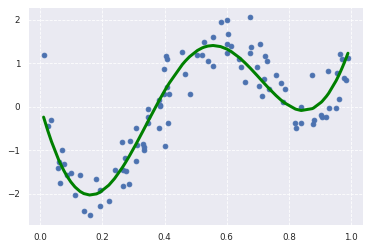
こちらもうまく予測できてそうです。

ちなみに、正則化なしでガウス基底関数のみを使用した分析はどうでしょうか。

スクリプト

from sklearn.kernel_ridge import KernelRidge

clf = KernelRidge(alpha=0, kernel='rbf')
clf.fit(data, target)

p_kridge = clf.predict(data)

plt.scatter(data, target, color='blue', label='data')

plt.plot(data, p_kridge, color='orange', linestyle='-', linewidth=3, markersize=6, label='kernel ridge')
plt.legend()

print("R^2：",clf.score(data,target))

出力

R^2： 0.999999999999924

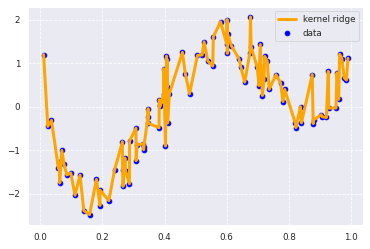
決定変数が1にすごく近い！良いモデルだ！
とはならず、グラフを見ると過学習を起こしています。
この状態では、未知のデータに対しては、うまく予測できないことがわかると思います。

正則化によってうまくこの状態を回避されていることがわかります。

4. おまけ

リッジ正則化とラッソ正則化を合わせたものをElastic Netといいます。

\(S_γ = (y - Φw)^T(y - Φw) + γ_1||w||_1 + γ_2||w||_2\)

5. 最後に

ラビットチャレンジでの講義である非線形回帰モデルについてまとめました。
回帰モデルについてはこれで終了です。

また、いつものごとく色々数学的に突っ込みどころがありそうなまとめ方ですが、
ご了承ください。。

次回、機械学習③：ロジスティック回帰についてまとめていきたいと思います。